Code
# Import seaborn with alias sns
import pandas as pd
import seaborn as sns
# Import matplotlib.pyplot with alias plt
import matplotlib.pyplot as pltkakamana
January 8, 2023
We will learn the basics of this popular statistical model, what regression is, and how linear and logistic regressions differ. We’ll then learn how to fit simple linear regression models with numeric and categorical explanatory variables, and how to describe the relationship between the response and explanatory variables using model coefficients
This Simple Linear Regression Modeling is part of Datacamp course: Introduction to Regression with statsmodels in Python
This is my learning experience of data science through DataCamp
| dist_to_mrt_m | n_convenience | house_age_years | price_twd_msq | |
|---|---|---|---|---|
| 0 | 84.87882 | 10 | 30 to 45 | 11.467474 |
| 1 | 306.59470 | 9 | 15 to 30 | 12.768533 |
| 2 | 561.98450 | 5 | 0 to 15 | 14.311649 |
| 3 | 561.98450 | 5 | 0 to 15 | 16.580938 |
| 4 | 390.56840 | 5 | 0 to 15 | 13.040847 |
Before diving into Regression we need to have brief overview of Descriptive statistics
Descriptive statistics: An example of descriptive statistics would be a summary of a given data set, which can be either a complete representation of a population or a sample of that population. There are two types of descriptive statistics: measures of central tendency and measures of variability (spread). The mean, median, and mode are measures of central tendency, whereas the standard deviation, variance, minimum and maximum variables, kurtosis, and skewness are measures of variability
Variables & their relationship:
While finding relationship b/w two variables (there can be more than two variables, but lets stick to two variable consideration for this article), we can identify following type of variables:
x = independent / explanatory variable
y = dependent / response variable.Regression: A regression is a statistical technique that relates a dependent variable to one or more independent (explanatory) variables
Types of regression: * Linear regression: The response variable is numeric. * Logistic regression: The response variable is logical.
In simple linear/logistic regression, there is only one explanatory variable
In python there are two packages / libraries for regression mostly uses are: * statsmodel: Optimized for insights * scikit-learn: Optimized for prediction
We’ll look at the relationship between house price per area and the number of nearby convenience stores using the Taiwan real estate dataset.
One challenge in this dataset is that the number of convenience stores contains integer data, causing points to overlap. To solve this, you will make the points transparent.
# Draw the scatter plot
sns.scatterplot(x='n_convenience', y='price_twd_msq', data=taiwan_real_estate)
# Draw a trend line on the scatter plot of price_twd_msq vs. n_convenience
sns.regplot(x="n_convenience", y="price_twd_msq", data=taiwan_real_estate,
ci=None,
scatter_kws={'alpha': 0.5})
# Show the plot
plt.show()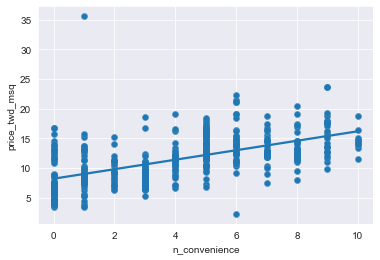
Straight lines are defined by two things:

While sns.regplot() can display a linear regression trend line, it doesn’t give you access to the intercept and slope as variables, or allow you to work with the model results as variables. That means that sometimes you’ll need to run a linear regression yourself.
# Import the ols function
from statsmodels.formula.api import ols
# Create the model object
mdl_price_vs_conv = ols("price_twd_msq ~ n_convenience", data=taiwan_real_estate)
# Fit the model
mdl_price_vs_conv = mdl_price_vs_conv.fit()
# Print the parameters of the fitted model
print(mdl_price_vs_conv.params)Intercept 8.224237
n_convenience 0.798080
dtype: float64Variables that categorize observations are known as categorical variables. Known as levels, they have a limited number of values. Gender is a categorical variable that can take two levels: Male or Female.
Numbers are required for regression analysis. It is therefore necessary to make the results interpretable when a categorical variable is included in a regression model.
A set of binary variables is created by recoding categorical variables. The recoding process creates a contrast matrix table by “dummy coding”
There are two type of data variables: * Quantitative data: refers to amount * Data collected quantitatively represents actual amounts that can be added, subtracted, divided, etc. Quantitative variables can be: * discrete (integer variables): count of individual items in record e.g. No. of players * continuous (ratio variables): continuous / non-finite value measurements e.g. distance, age etc * Categorical: refers to grouping There are three types of categorical variables: * binary: yes / no e.g. head/tail of coin flip * nominal: group with no rank or order b/w them e.g. color, brand, species etc * ordinal: group that can be ranked in specific order e.g. rating scale in survey result
If the explanatory variable is categorical, the scatter plot that you used before to visualize the data doesn’t make sense. Instead, a good option is to draw a histogram for each category.
# Histograms of price_twd_msq with 10 bins, split by the age of each house
sns.displot(data=taiwan_real_estate,
x='price_twd_msq',
col='house_age_years',
bins=10)
# Show the plot
plt.show()
print("\nIt appears that new houses are the most expensive on average, and the medium aged ones (15 to 30 years) are the cheapest.")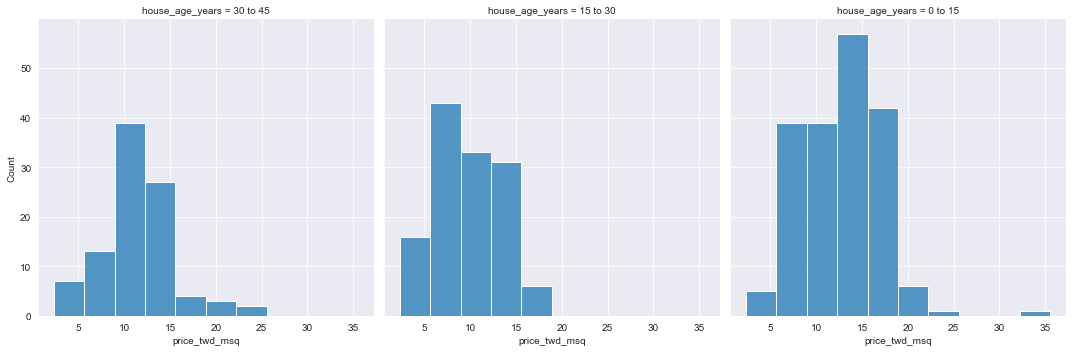
It appears that new houses are the most expensive on average, and the medium aged ones (15 to 30 years) are the cheapest.Using summary statistics for each category is a good way to explore categorical variables further. Using a categorical variable, you can calculate the mean and median of your response variable. Therefore, you can compare each category in more detail.
house_age_years
0 to 15 12.637471
15 to 30 9.876743
30 to 45 11.393264
Name: price_twd_msq, dtype: float64While calculating linear regression with categorical explanatory variable, means of each category will also coefficient of linear regression but this hold true in case with only one categorical variable. Lets verify this
Intercept 12.637471
house_age_years[T.15 to 30] -2.760728
house_age_years[T.30 to 45] -1.244207
dtype: float64# Update the model formula to remove the intercept
mdl_price_vs_age0 = ols("price_twd_msq ~ house_age_years + 0", data=taiwan_real_estate).fit()
# Print the parameters of the fitted model
print(mdl_price_vs_age0.params)
print("\n The coefficients of the model are just the means of each category you calculated previously. Fantastic job! ")house_age_years[0 to 15] 12.637471
house_age_years[15 to 30] 9.876743
house_age_years[30 to 45] 11.393264
dtype: float64
The coefficients of the model are just the means of each category you calculated previously. Fantastic job!